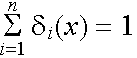FUZZEKS [to Index]
Fuzzy Kriging: Basics / Theoretical concepts
Kriging belongs to the most popular methods of spatial interpolation of data.
The fuzzy kriging abilities of FUZZEKS are based on a modification of the
conventional kriging procedure. The difference is that fuzzy kriging (of the
type FUZZEKS uses) additionally allows the use of imprecise input data
(e.g. estimations obtained from an expert).
Imprecise data are represented in FUZZEKS by fuzzy numbers.
Fuzzy numbers (definition)
The definition of a fuzzy number is based on the definition of a fuzzy set.
A fuzzy set of a set X is defined by a membership function m
that supplies for each value of X a so-called membership value
in the range [0,1].
m : X -> [0,1]
It is similar to a subset of X, except each element x of X
can not only be (m(x)=1) or not be (m(x)=0) element of the fuzzy set,
but also can be element gradually (0<m(x)<1).
See also references at bottom of
Overview/References.
A fuzzy set of R (the real numbers) is called a fuzzy number
if the membership function m
is convex and m(x)=1 for exactly one point x of R.
(Convex means that the function decreases monotonically to both sides of the
point where the value 1 is taken.)
Have a look at
"Load Input File / FDF-inputfile-format"
for further details on how to formulate fuzzy input data for FUZZEKS.
- Example: Definition of a fuzzy number 4.
If values of the parameter x
can not be lower than 2 and not greater than 5 then a membership
function may look like:

(In this example: m(2)=0, m(3)=0.5, m(4)=1, etc.)
For FUZZEKS one could define this fuzzy number in the form
4 / 0: 2-5
(first the point where the membership function takes the value 1,
then the range of values with membership values grater than 0).
Remark: The conventional crisp real
numbers can be embedded in the set
of fuzzy numbers,
so that crisp numbers are a special case of fuzzy numbers.
Their membership function
is 1 for the given real number
and 0 for all other real numbers.
This is because a crisp real number always
expresses only this number
(all other numbers are impossible,
so the membership value is 0).
Fuzzy kriging procedure
The input for fuzzy kriging are values of parameters
(either exact or imprecise) at given points
(the parameters that are to be estimated).
The output of fuzzy kriging is an estimated value for any specified
location.
Fuzzy kriging is based on a theoretical variogram which is result of
a statistical analysis of the parameter.
It tells about the similarity of values with respect to their distance.
The experimental variogram (calculated utilizing the input data) is used
as a statistical tool to find the theoretical variogram.
FUZZEKS can calculate it taking the fuzziness into account (which yields
a fuzzy experimental variogram),
although the theoretical variogram can only be crisp.
The reason is that the user can take the fuzziness into account when fitting
a theoretical variogram curve.
- Remark: The experimental (semi)variogram can be formulated as

where the xi are the input coordinates, the Z(xi) are the input values
which can take a form of fuzzy numbers mentioned above, and h is the
distance-vector between points. In practice the direction of the
distance-vector is not taken into account (in this case the vector xi-xj
is replaced by the distance of xi and xj).
To facilitate the kriging procedure FUZZEKS offers
Theoretical concepts of fuzzy kriging
The rest of this page deals with the (mathematical) assumptions that are
made for simple point kriging. Also, it roughly describes how the
assumptions lead to the spatial kriging estimations.
The following description is valid for the crisp case. If fuzzy values are
used, the Extension Principle (well known in fuzzy theory,
see also references at bottom of Overview/References,
especially [Zadeh, 1965]) is used to convert
the main kriging equation (3 headlines below) into a fuzzy function.
(If you want to have a rough description of the application of the
extension principle, have a look at the
Overview of membership function window.)
Below (at the main kriging equation) is an additional remark regarding
the fuzzy version of the main kriging equation.
Notations
x: Location in 2-dimensional space
Z(x): Input parameter value at the location x
Z (x): Estimated value at the location x
(x): Estimated value at the location x
xi: Locations where an input parameter value exists (i=1..n)
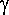 (x1,x2)=
(x1,x2)=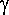 (x1-x2): The
semivariogram (=VAR(Z(x1)-Z(x2))/2), which is the same as the earlier
definition of the experimental variogram because of the following
assumptions
(x1-x2): The
semivariogram (=VAR(Z(x1)-Z(x2))/2), which is the same as the earlier
definition of the experimental variogram because of the following
assumptions
 : Kriging variance at the location x
( E((Z(x)-Z
: Kriging variance at the location x
( E((Z(x)-Z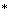 (x))^2) )
(x))^2) )
Assumptions
(1) E(Z(x))=m
The expected parameter value exists and does not depend on x.
(2) VAR(Z(x+h)-Z(x))/2=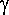 (h)
(h)
The difference Z(x+h)-Z(x) has finite variance
and does not depend on x.
Main kriging equation
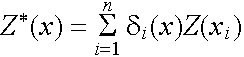 The estimated value is a linear combination of the input values and
the coefficients
The estimated value is a linear combination of the input values and
the coefficients 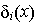 . The
. The 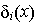 are calculated by using the
assumptions with a user-supplied theoretical (semi)variogram.
are calculated by using the
assumptions with a user-supplied theoretical (semi)variogram.
(Remark: For a fixed x the coefficients 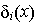 are variables of
real numbers only.)
are variables of
real numbers only.)
Remark for the case of fuzzy input values Z(x):
The 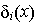 are crisp values although the input values are fuzzy
(in the case of a crisp theoretical variogram, which is true for FUZZEKS
as described above);
they can be obtained by the crisp solution (which is described below).
are crisp values although the input values are fuzzy
(in the case of a crisp theoretical variogram, which is true for FUZZEKS
as described above);
they can be obtained by the crisp solution (which is described below).
Calculation of the 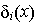
The assumptions and the demand
E(Z(x)-Z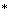 (x)) = 0
(x)) = 0
lead to two equations:
(1) 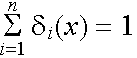
(2) 
The 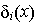 are chosen in a way that a minimal
estimation variance (2) will be obtained (observing (1)).
are chosen in a way that a minimal
estimation variance (2) will be obtained (observing (1)).
Remark: Minimizing (2) gives n equations (the n differentials equal zero)
and (1) is one more equation.
Remark: Using the Lagrange principle, one can solve these equations
(unique solution). A unique solution can always been found because of
the selection of theoretical variograms that is allowed by FUZZEKS.
FUZZEKS allows to use kriging by offering


 (x): Estimated value at the location x
(x): Estimated value at the location x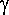 (x1,x2)=
(x1,x2)= : Kriging variance at the location x
( E((Z(x)-Z
: Kriging variance at the location x
( E((Z(x)-Z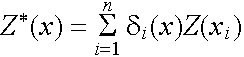 The estimated value is a linear combination of the input values and
the coefficients
The estimated value is a linear combination of the input values and
the coefficients 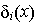 . The
. The